Władysław WitwickiMyślenie

„Myśleć” to wyraz dwuznaczny. Bo raz znaczy tyle, co przedstawiać sobie coś, a raz wychodzi na to samo, co sądzić lub suponować, że coś istnieje lub nie istnieje. Dlatego chcąc mówić o myśleniu, musimy się bliżej zapoznać z sądami i pojęciami.

Podział sądów

Znamy już zjawisko duchowe zwane sądem i wiemy, że w każdym sądzie albo uznajemy istnienie czegoś, albo zaprzeczamy, żeby coś istniało. Dlatego odróżniamy sądy twierdzące i sądy przeczące. Każdy sąd dotyczy czegoś, innymi słowy: ma jakiś przedmiot, który albo istnieje naprawdę, albo go nie ma. Dlatego dzielimy sądy na prawdziwe i mylne. Każdy sąd, który wydajemy, uważamy tym samym za prawdziwy. Pamiętajmy tylko, że wydawać sąd to nie znaczy wypowiadać go, pisać czy jak inaczej go objawiać, tylko to znaczy: myśleć serio, że jest tak i tak, być przeświadczonym, że tak jest, być pewnym, że jest tak, a nie inaczej. Prawdziwy jest sąd twierdzący, którego przedmiot istnieje, i każdy sąd przeczący, którego przedmiot nie istnieje. Innymi słowy: jeżeli jest tak w rzeczywistości, jak myślisz, że jest, twój sąd jest prawdziwy. To samo krócej: sądy zgodne z rzeczywistością nazywają się prawdziwe, a niezgodne z rzeczywistością nazywają się mylne, czyli fałszywe.

Prawda i fałsz

Prawda, Obraz świata, SłowoPrawda jest to zgodność naszych myśli z rzeczywistością, a nie: zgodność naszych słów z naszymi myślami. To ostatnie nazywa się prawdomównością, szczerością, otwartością, sztuką wymowy i zależy od dobrych chęci mówiącego i od jego sprawności stylistycznej, a to, czy moje sądy są prawdziwe, czy mylne, nie zależy ani od moich chęci, ani od mojej wprawy w wyrażaniu myśli. Kto mówi inaczej, niż myśli, ten kłamie, albo nie umie mówić. Kto się myli i tak mówi, jak myśli, ten nie kłamie, tylko mówi nieprawdę nieświadomie. Więc jeżeli z czyichś ust usłyszysz zdania, które ci się wydadzą niezgodne z rzeczywistością, nie myśl zaraz, że ten ktoś kłamie. Może on się tylko myli, a mylić się może każdy z nas. To rzecz ludzka. A może się tylko źle wyraża?

KłamstwoKłamstwo — to umyślne i świadome wprowadzanie kogoś w błąd, świadome wywoływanie u drugich ludzi sądów mylnych. To można czasem zrobić nawet przez wypowiadanie zdań prawdziwych, ale takim tonem i w takich okolicznościach, że nikt tych zdań nie weźmie serio, tylko będzie myślał, że to są żarty, przekora, a nie, że to jest nieoczekiwana prawda.

Błądzenie, Grzeczność, NaukaPonieważ każdy z nas może się mylić i nigdy nie wie o tym w danej chwili, że właśnie jest w błędzie, a być w błędzie to jest na ogół stan godny pożałowania, dlatego unikamy w rozmowie towarzyskiej zwrotu: „Pan się myli”. Nie można takich zwrotów uniknąć w polemice naukowej i tam się nikt nie powinien o nie obrażać.

Jeżeli nasz sąd dotyczy wszystkich przedmiotów jakiegoś rodzaju albo jakiegoś przedmiotu w całości, wtedy nazywa się sądem ogólnym. Jeżeli dotyczy przynajmniej niektórych przedmiotów pewnego rodzaju, nazywa się sądem szczegółowym. Sądy ogólne twierdzące to np. takie, jak: „wszystkie owady mają szkielet zewnętrzny”, albo: „wszystkie ptaki rozmnażają się z jaj”, albo: „Napoleon I był cesarzem Francuzów”, a szczegółowe twierdzące to takie, jak: „niektóre ssaki składają jaja” albo: „zdarzają się łabędzie czarne”. Ogólne przeczące to np.: „żadna ryba nie oddycha płucami”, albo: „żadna z naszych żab nie kąsa”. Szczegółowe przeczące to np. takie: „niektóre kręgowce nie oddychają płucami” lub: „niektóre kwiaty nie pachną”. Tak samo gdy chodzi nie o zwierzęta, tylko o jakikolwiek inny rodzaj przedmiotów. Wyraz „niektóre” znaczy: „przynajmniej niektóre”, a nie znaczy: „tylko niektóre”.

Powiedzenia

Sądy wyrażamy przy pomocy zdań mówionych lub pisanych. Nie wszystkie zdania wyrażają sądy. Niektóre zdania wyrażają rozkazy, prośby lub pytania. Te, które wyrażają sądy, nazywają się zdaniami orzekającymi lub powiedzeniami.

Powiedzenia wyrażające sądy prawdziwe nazywają się też prawdziwe, a które wyrażają sądy fałszywe nazywają się powiedzeniami fałszywymi.

Pozory, ŻartNiekiedy zdania orzekające brzmią tak, jakby wyrażały sądy, ale ton ich i zachowanie się tego, który je wypowiada, świadczą, że on w głębi duszy nie myśli tak, jak mówi. Np. kiedy dzieci śpiewają: „Budujemy mosty dla pana starosty”, wcale nie myślą, żeby coś budowały naprawdę; one myślą tak na niby. Ich zdania nie wyrażają sądów, tylko supozycje[1]. Podobnie bywa i u dorosłych. Dlatego nie można wszystkiego, co ktoś mówi, brać za wyraz jego sądów, przekonań. W rozmowie pokaże się nieraz, że ten ktoś wyrażał tylko swoje supozycje, czyli sądy na niby. To samo może pokazać jego postępowanie.

Supozycje też, a nie sądy, wyrażają powiedzenia, w których wyrażamy swoje przypuszczenia, wątpienia i myśli cudze, do których się sami nie przyznajemy. Na przykład: „Przypuszczam, że jeszcze zdążę do pociągu”, albo: „Wątpię, czy do października skończę tę robotę”, albo: „Oskarżony twierdzi, że jest niewinny”. Kiedy przypuszczamy tylko, a nie jesteśmy pewni czegoś, wtedy nie przeżywamy sądów, tylko supozycję pewną i czujemy, że potrafilibyśmy bez wielkiej trudności przeżyć i sąd tej treści. Kiedy tylko wątpimy w coś, ale nie przeczymy, wtedy też przeżywamy supozycję i czujemy, że moglibyśmy wydać i sąd przeczący danej treści, choć go jeszcze nie wydajemy. Tak samo kiedy powtarzamy cudze zdania, nie biorąc ich na swoją odpowiedzialność, kiedy podajemy pewne zdania tylko dla przykładu, aby rozwiązać jakieś zadanie rachunkowe, ale nie myślimy, że np. jakiś chłopiec naprawdę kupił cztery bułki lub coś podobnego. Zdania wypowiadamy i wtedy, ale one nie wyrażają naszych sądów, tylko supozycje.

Powiedzenia bywają jasne i niejasne. Niejasne są wtedy, gdy zawierają wyrazy, które można rozumieć rozmaicie, albo takie, które nie wiadomo, jak należy rozumieć. Tak np. zdanie wyrwane z dłuższego opowiadania: „Zamek zapewniał mu bezpieczeństwo” musi być niejasne, jak długo nie wiemy, czy chodzi w nim o zamek u drzwi, czy o zamek murowany. To wyjaśnia dopiero treść opowiadania. Albo Prawda, Fałszzdanie wyjęte z artykułu o pewnym autorze: „Autor posiada w dość wysokim stopniu to, co Francuzi nazywają esprit littéraire”. Tu zupełnie nie wiadomo, co autor posiada i w jakim stopniu. O powiedzeniach niejasnych nie można wiedzieć, czy są prawdziwe, czy fałszywe. Natomiast każde powiedzenie jasne jest albo prawdziwe, albo fałszywe. Dlatego nie należy się nigdy spierać o to, czy jest prawdą, czy nie jest prawdą pewne powiedzenie, dopóki nie wiadomo dobrze, czy ono znaczy to, czy tamto. Dlatego chcąc ocenić, czy zdanie czyjeś jest prawdziwe czy mylne, trzeba się naprzód zastanowić, czy rozumiemy każde słowo użyte w tym zdaniu, i jeśli to jest możliwe, żądać naprzód wyjaśnienia wyrazów, a potem dopiero wydawać sąd o tym, co słyszymy lub czytamy. Tak samo we własnych myślach musimy uważać na to, czy sobie przedmiot sądu przedstawiamy jasno czy tylko mętnie, mglisto, chwiejnie. Dopiero wtedy możemy sami wiedzieć, jaki właściwie sąd wydajemy i co mamy na myśli. Nieraz mętne powiedzenia wyglądają na głębokie, doniosłe prawdy i ludzie wielkie przez to ponoszą szkody.

Pojęcia naukowe

SłowoKiedy nam zależy na tym, żeby poznać jakiegoś rodzaju rzeczy i nie narażać się na pomyłki i nieporozumienia z drugimi, kiedy o tych rzeczach mowa, staramy się określać znaczenie wyrazów, którymi się posługujemy. Tak np. ucząc się geometrii, dowiadujemy się, że kwadrat to jest figura płaska, czworoboczna, prostokątna, równoboczna, a nie co bądź graniastego, że koło to linia krzywa, płaska i zamknięta, której wszystkie punkty są jednakowo oddalone od środka, a nie, że to jest coś okrągłego. Przedtem wiązaliśmy z wyrazem „kwadrat” niejasne wyobrażenie pochodne, raz takie, raz inne, i posługując się tym wyrazem, nie mogliśmy być pewni, że ktoś drugi wiąże z tym wyrazem takie samo wyobrażenie pochodne i ten sam przedmiot ma na myśli, co i my. Jeżeli obaj rozmawiający znają określenie kwadratu podane w geometrii, mogą z sobą rozmawiać bez obawy nieporozumienia; każdy z nich wiąże teraz z wyrazem „kwadrat” takie samo przedstawienie i to samo ma na myśli, choćby w danej chwili nie miał żadnego wyobrażenia pochodnego albo je miał niewyraźne.

Przedstawienia nieobrazowe, w których dobrze wiemy, co właściwie mamy na myśli, i potrafimy, przeżywając je, zawsze to samo mieć na myśli, nazywają się pojęciami naukowymi. Ustalamy je przy pomocy jasnych określeń, zwanych definicjami. Tu przed chwilą podaliśmy definicję kwadratu i definicję koła. W nauce chemii znaleźć możemy definicję soli lub wody, w nauce gramatyki definicję podmiotu, w botanice definicję pręcików i słupków kwiatowych, procesu asymilacji[2] itd.

Oczywiście, że definicja, jeżeli ma się na coś przydać, nie powinna sama zawierać tego wyrazu, który ma określać. Na przykład: „kwadrat to jest kwadratowa powierzchnia” albo: „masło to jest taka maść maślana do jedzenia i do gotowania”. Kto by naprawdę nie wiedział, jak ma rozumieć wyrazy „kwadrat” i „masło”, nie dowie się z takich określeń, jak ma te wyrazy rozumieć.

Dobra definicja daje się zawsze odwrócić w ten sposób, że w niej podmiot i orzeczenie mogą ze sobą zamieniać miejsca, a zdanie zostanie prawdziwe. Np.: „figura płaska czworoboczna, równoboczna i równokątna jest kwadratem” albo: „linia krzywa, płaska, zamknięta, której wszystkie punkty są równo oddalone od środka, jest kołem”. To są odwrócenia podanych przed chwilą definicji kwadratu i koła i są zdaniami prawdziwymi, bo podane definicje były poprawne.

Gdyby ktoś powiedział, że kwadrat to jest figura płaska, czworoboczna, byłaby to definicja za obszerna, bo obejmowałaby oprócz kwadratów także i prostokąty, i romby. Gdyby zaś powiedział, że kwadrat to figura płaska, czworoboczna, równoboczna i równokątna o boku równym jednemu metrowi, byłaby to definicja za ciasna, bo nie obejmowałaby wszystkich kwadratów, większych i mniejszych, tylko niektóre.

W życiu nie ma powodu żądać od każdego, z kim mówimy, definicji każdego wyrazu, jakiego ktoś w zdaniu użyje. Np. łyżka, sos, książka, stół… Nie trzeba udawać, że się rozumie mniej, niż się rozumie naprawdę, ale tam, gdzie nie jesteśmy pewni, czy rozumiemy kogoś dobrze i czy nie zachodzi między nami jakieś nieporozumienie, trzeba koniecznie ustalić naprzód znaczenia wyrazów niejasnych, którymi się posługujemy, a dopiero potem zgadzać się lub się nie zgadzać.

Słowo, FilozofWyrazy, których znaczenie jest ustalone przy pomocy definicji, nazywają się terminami. Każda definicja mówi, jak należy rozumieć pewien termin, czyli ustala jego znaczenie. Innymi słowy: mówi, co mamy sobie myśleć o przedmiocie, którego dany termin dotyczy. To znaczy, że ustala treść danego pojęcia.

Pojęcia pozwalają nam wydawać sądy prawdziwe nie tylko o jednym przedmiocie, ale o każdym przedmiocie pewnego rodzaju. Pojęcia przecież powstają w ten sposób, że na wielkiej ilości przedmiotów zaczynamy wyróżniać coś jednego, co im wszystkim przysługuje, i to coś potrafimy sobie przedstawiać osobno. To może być pewien kształt albo pewna barwa, albo pochodzenie, albo sposób życia, albo wartość, albo jakakolwiek inna cecha wspólna wielu przedmiotom, które dzięki tej cesze wyróżnionej zaliczamy do jednego rodzaju. Obraz świata, FilozofCzynność wyróżniania jakiejś cechy wspólnej wielu przedmiotom nazywa się odrywaniem jej lub z łacińska abstrakcją. Abstrakcjami też lub pojęciami oderwanymi nazywają się pojęcia takie jak kształt, wielkość, budowa, symetria, piękność, czas trwania, bo te cechy nie występują nigdy same dla siebie, każda z osobna, tylko zawsze razem z innymi połączone w całość na przedmiotach wyobrażeń. Przedmioty te wyglądają, jakby były zrośnięte ze swoich cech. Dlatego się nazywają z łacińska przedmiotami konkretnymi. (Po łacinie „concresco” znaczy: zrastam się). Cechy wyróżnione na przedmiotach konkretnych możemy w myśli łączyć w nowe grupy i w ten sposób tworzyć pojęcia syntetyczne[3]. Do tego potrzeba fantazji. Np. ptak wielkości góry, jaszczurka zionąca ogniem i skrzydlata, kula o promieniu 6000 km itd.

Wszystkie przedmioty podpadające pod pewne pojęcie stanowią razem jego zakres. Tak np. wszystkie możliwe kwadraty stanowią zakres pojęcia „kwadrat”, a wszystkie koty, jakie tylko są, stanowią zakres pojęcia „kot”.

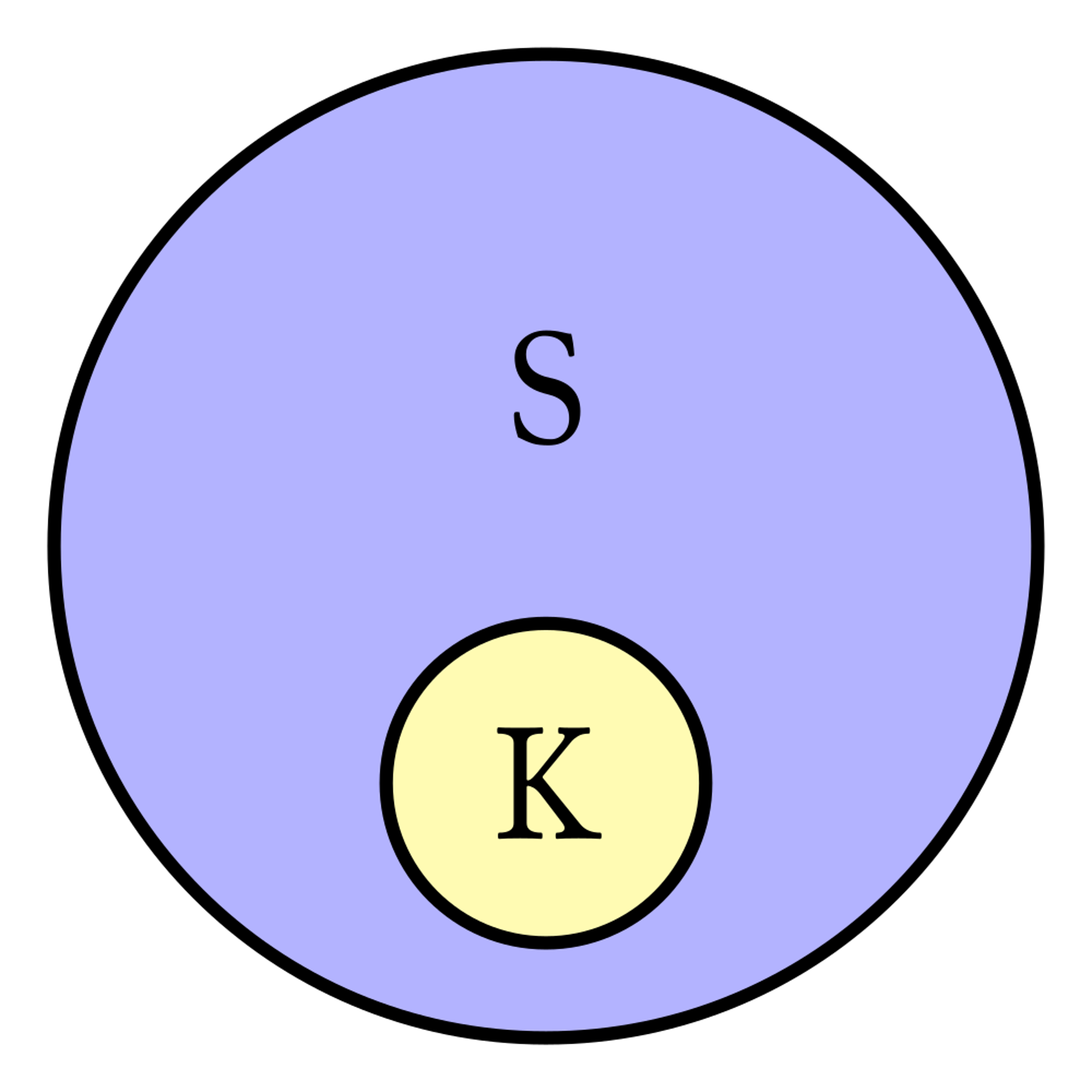
Zakresy pojęć zostawać mogą do siebie w różnych stosunkach. Tak np. wiemy, że wszystkie koty są ssakami, choć nie wszystkie ssaki są kotami. Tutaj zakres pojęcia „kot” jest częścią zakresu pojęcia „ssak”. Można zakresy tych pojęć przedstawić w postaci dwóch kół, z których mniejsze mieści się w obwodzie koła większego (zob. rys. 1).

Takie dwa pojęcia zostają w stosunku podporządkowania. Podobnie pojęcia: stół i mebel, bigos i potrawa, szabla i broń, głowa i część ciała i wiele innych. Inny stosunek zachodzi np. między pojęciem „guzika” a pojęciem „przedmiotu z rogu”. Bo tylko niektóre guziki są z rogu, a niektóre nie i tylko niektóre przedmioty z rogu są guzikami, a niektóre nie są. Taki stosunek można przedstawić przy pomocy dwóch kół, których obwody się krzyżują i on się też nazywa stosunkiem krzyżowania się (zob. rys. 2).

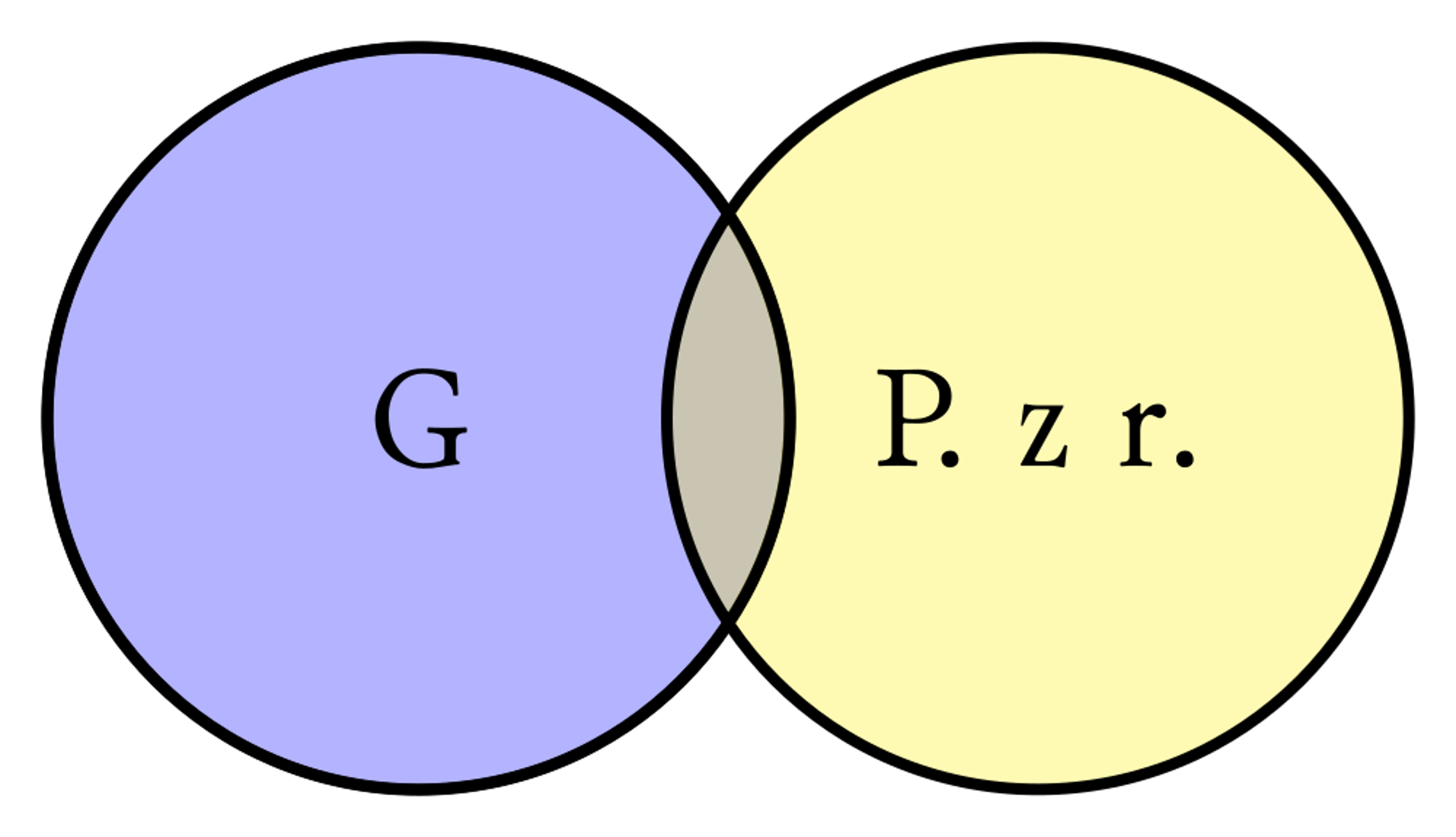
Bywa też tak, że żaden z przedmiotów należących do zakresu jednego pojęcia nie należy do zakresu pojęcia drugiego. Wtedy mówimy o stosunku wykluczania się. Ten może być dwojaki. Bo może być tak, że oprócz zakresów tych dwóch pojęć istnieją jeszcze zakresy pojęć innych, za czym to, co nie należy do zakresu jednego z nich, nie musi zaraz mieścić się w zakresie drugiego. Np. weźmy takie dwa jak ryba i ptak. To prawda, że co jest rybą, to nie jest ptakiem, i co ptak, to nie ryba, ale może coś być ani rybą, ani ptakiem, na przykład: płaz albo ssak, albo ślimak, albo parasol, albo liczba parzysta. Taki stosunek wykluczania się dwóch pojęć nazywa się przeciwieństwem (zob. rys. 3).

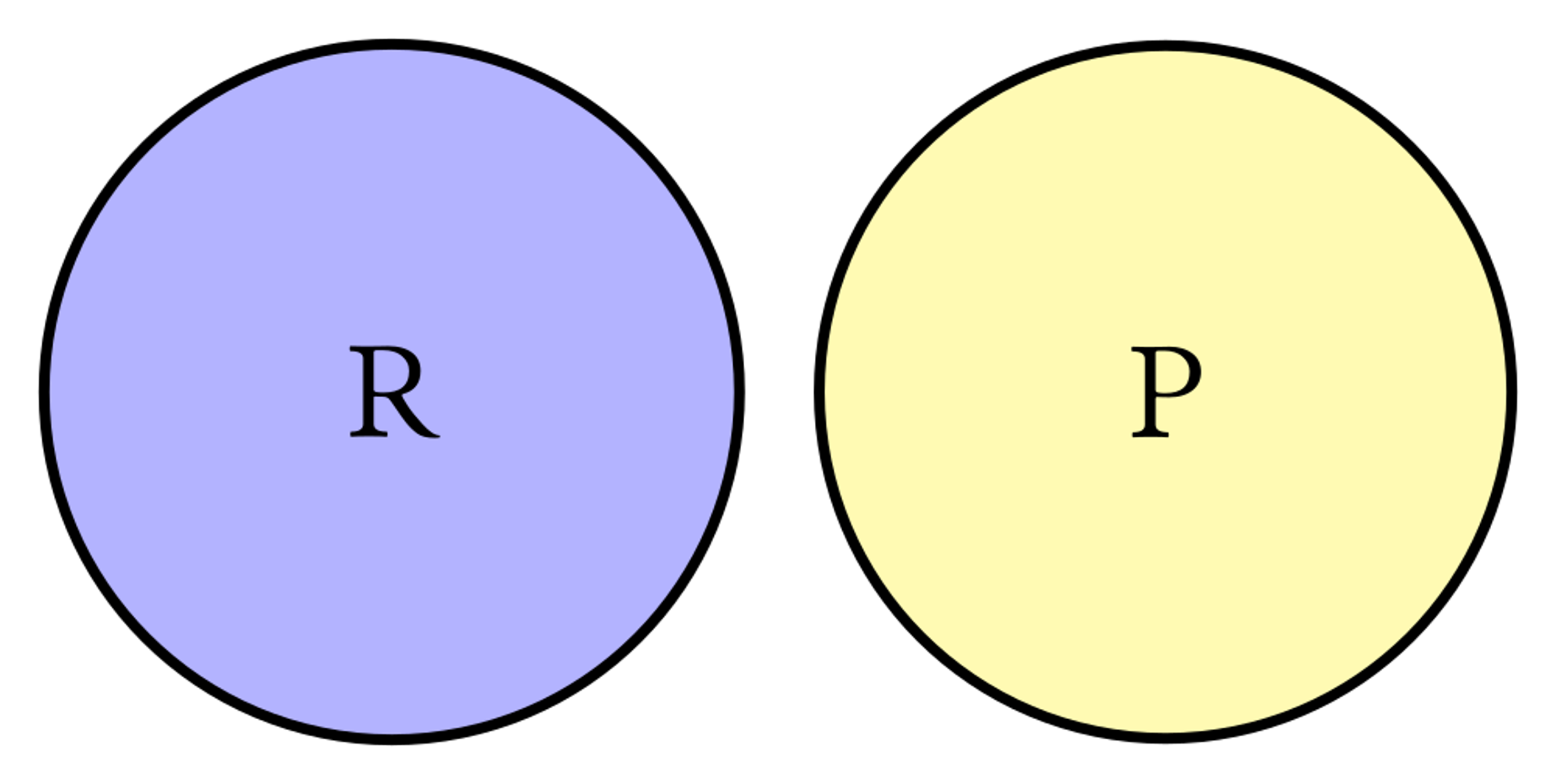
A może być tak, że co nie należy do zakresu jednego z dwóch pojęć, to już tym samym należy do zakresu drugiego z nich. Między takimi dwoma pojęciami zachodzi stosunek sprzeczności. Np. kwadrat i nie-kwadrat, pies i nie-pies, człowiek i nie-człowiek. Taki stosunek można przedstawić za pomocą jednego koła i całej powierzchni poza jego obwodem (zob. rys. 4). Cokolwiek nie leży w obrębie koła N, to leży w przestrzeni nie-N. Każdy przedmiot albo jest N, albo nie-N i nie ma trzeciego wyjścia. Co nie jest człowiekiem, to jest nie-człowiekiem. Wszystko jedno, czy byłaby to lokomotywa, czy rachunek jakiś, czy litera, czy cokolwiek bądź innego. Jakiekolwiek pojęcie weźmiemy i drugie, które jest jego zaprzeczeniem — zawsze w zakresach tych obu pojęć razem mieści się wszystko, o czym tylko pomyślimy.

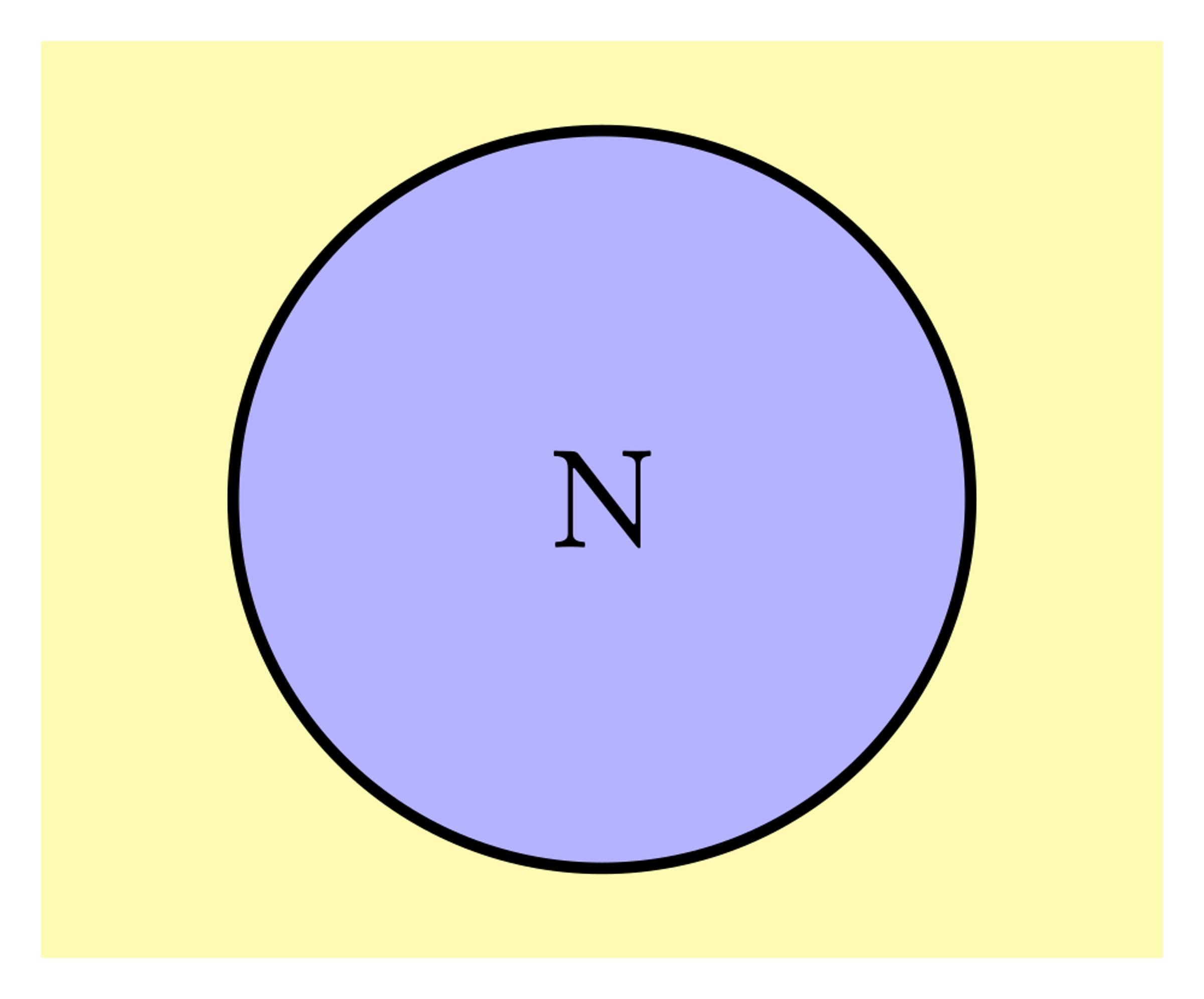
Dobrze jest umieć dostrzegać pojęcia przeciwne i pojęcia sprzeczne. Bo można czasem wahać się co do tego, czy coś jest rybą, czy nie-rybą, jeżeli się tego stworzenia nie zna, ale jeśli by ktoś utrzymywał, że coś było i rybą, i nie-rybą zarazem, albo rybą i ssakiem równocześnie, albo człowiekiem i nie-człowiekiem naraz, ten się na pewno myli i nie warto się o to spierać, czy było coś takiego czy nie było. Żaden przedmiot nie należy do zakresu dwóch pojęć, które się wykluczają.

Mimo to u poetów, w zabawach, w snach i w podaniach chętnie spotykamy opowiadania i obrazy dotyczące np. wilka, który mówi po ludzku i można mu brzuch rozpruć, wyjąć z niego babcię i wnuczkę, a wypakować go kamieniami, po czym wilk biegnie do studni i tam się topi. Nic nam to nie przeszkadza, że taki wilk musiałby być i nie-wilkiem równocześnie i żywym stworem, który coś zjada, i nieżywym workiem, który można bez protestu z jego strony rozpruwać i zaszywać, i musiałby w swoim brzuchu mieścić dwie osoby większe od niego całego. To wszystko są rysy sprzeczne, które w bajce, w supozycjach nie rażą. Tylko na jawie, kiedy chodzi o rzeczy ważne, trzeba się wystrzegać, żeby się przedmioty naszych sądów nie okazywały przedmiotami sprzecznymi, bo wtedy ich na pewno nie ma i my jesteśmy w błędzie.

W końcu jeszcze jeden stosunek między pojęciami można przedstawić jednym kołem. To wtedy, gdy dwa pojęcia mają różną treść, ale ten sam zakres. Tak się dzieje, gdy tę samą rzecz lub zbiór rzeczy umiemy dwojako pojmować. Tak np. „zwycięzca, który wygrał bitwę pod Jeną” i „pierwszy cesarz Francuzów”. Treść tych pojęć różna, ale zakres ten sam. Stanowi go osoba Napoleona I, pojęta raz tak, raz inaczej. Podobnie można pojąć wodę jako związek chemiczny tlenu i wodoru według wzoru H₂O, a można też ją pojąć jako najtańsze podłoże dla transportów. Będą to pojęcia też różnej treści, a zakres ich ten sam: woda. Oba koła nakrywają się i tutaj widać na rysunku tylko jedno koło z dwoma znaczkami. Takie dwa pojęcia nazywają się zamienne (zob. rys. 5).

Jeżeli ktoś umie łatwo i szybko zdawać sobie sprawę ze stosunków między pojęciami, które spotyka w rozmowie albo w książce, wielki ma z tego pożytek, bo łatwiej mu wtedy myśleć, mówić i pisać jasno.

Związki logiczne między sądami

Kłamstwo, Prawda, Fałsz, Obraz świata, SłowoWiadomo, że gdy się ktoś wypiera popełnionego czynu przed sądem, naraża się na to, że mu jednak popełnienie czynu udowodnią. Kiedykolwiek ktoś kłamie, naraża się na to, że się jego kłamstwo wyda. Ono się nieraz odsłania po krótkiej chwili, w ciągu rozmowy, kiedy mu tylko ktoś zacznie zadawać szereg pytań odpowiednio dobranych albo i kłamca sam zacznie mówić dalej i szerzej o tym, co miał spostrzec poza sobą albo i sam doznać. Kto chce skutecznie drugich w błąd wprowadzić przez wypowiedzenie jakiegoś zdania fałszywego, ten musi nie tylko o tym jednym zdaniu myśleć, ale o wielu innych równocześnie. A dlaczego tak jest? Dlatego, że prawdziwość jakiegokolwiek sądu i fałszywość nie chodzi samopas, tylko pociąga za sobą nieuchronnie prawdziwość i fałszywość innych sądów. Sądy zostają ze sobą w związkach ze względu na swoją prawdę i fałsz. Te związki nazywają się związkami logicznymi. Jest ich wiele rodzajów. Zajmuje się nimi nauka logiki, tutaj wymienimy tylko niektóre dla przykładu. I tak prawdziwość jakiegokolwiek sądu ogólnego twierdzącego o czymkolwiek pociąga za sobą nieuchronnie fałszywość sądu szczegółowego przeczącego o tym samym przedmiocie. Prawda, FałszNp. jeżeli jest prawdą, że wszyscy uczniowie pewnej klasy byli pewnego dnia obecni w szkole, to na pewno jest fałszem, jakoby niektórzy uczniowie nie byli tego dnia w szkole. A jeżeli prawdą jest to drugie, to na pewno nie jest prawdą pierwsze. Oba sądy tej postaci nie mogą być zarazem prawdziwe. Jeden z nich musi być fałszywy. I na odwrót, jeżeli jeden z takich dwóch sądów jest fałszywy, to musi być prawdziwy drugi. Nie mogą być oba naraz fałszywe. Takie dwa sądy nazywają się sprzeczne. Bo każdy z nich zaprzecza temu samemu, co drugi twierdzi. Tak jakby ktoś mówił: „to jest czarne”, a drugi by utrzymywał, że „to nie jest czarne”, i obaj myśleliby o tym samym przedmiocie, o tej samej jego stronie i o tym samym momencie.

Taki sam stosunek sprzeczności zachodzi między każdym sądem ogólnym przeczącym a szczegółowym twierdzącym. Na przykład: jeżeli prawdą jest, że żaden uczeń pewnej klasy nie był pewnego dnia w szkole, to musi być fałszem to, jakoby niektórzy uczniowie byli tego dnia w szkole. I zarazem jeżeli to nieprawda, że wtedy żadnego ucznia nie było w szkole, to oczywiście prawdą jest, że niektórzy wtedy tam byli. Oba sądy tej postaci nie mogą być zarazem fałszywe i nie mogą być zarazem prawdziwe. Jeden z nich musi być fałszem, a drugi prawdą. To wiemy na pewno, choć nieraz nie wiemy, który z nich jest prawdą, a który fałszem. Gdy dwóch ludzi żywi takiego rodzaju dwa przekonania, nie może nikt przyjść i powiedzieć słusznie: „Macie obaj rację”, ani też: „Mylicie się obaj”. Chyba że zachodzi jakieś nieporozumienie i każdy z dwóch spierających się inaczej rozumie jeden i ten sam wyraz, którym się obaj posługują. Wtedy nie zachodzi między nimi sprzeczność, tylko pozory sprzeczności.

Kto mówi lub pisze, że „po pewnym widowisku wszyscy poszli do domu, a kilka osób jeszcze zostało na miejscu”, ten mówi źle. Widocznie zapomniał, że w pierwszym zdaniu wysłał do domu wszystkich. Jeżeli to prawda, to nie jest prawdą, że niektórzy nie poszli do domu, tylko zostali na miejscu. Trzeba zawsze uważać i pamiętać, co się myślało przed chwilą, żeby się nasze myśli nie sprzeczały.

Prawda, FałszInny stosunek logiczny zachodzi między dwoma sądami ogólnymi, z których jeden jest twierdzący, a drugi przeczący. Np. jeden nauczyciel mógłby twierdzić, że wszyscy uczniowie pewnej klasy są pilni, a drugi, że żaden uczeń tej klasy nie jest pilny. Między takimi dwoma sądami zachodzi stosunek przeciwieństwa, a nie stosunek sprzeczności. Dlatego, że takie dwa sądy, choć nie mogą być zarazem prawdziwe, to jednak mogą być oba mylne. I tak najczęściej bywa. Wtedy mianowicie, gdy niektórzy uczniowie są pilni, a niektórzy nie są pilni. Między dwoma sądami naprawdę sprzecznymi nie było trzeciej możliwości. Między sądami przeciwnymi może się znaleźć coś trzeciego, co się pokaże prawdą, gdyby się one oba okazały mylne. Taki sam stosunek zachodzi np. między sądem: „ten stół jest dębowy” i drugim: „ten stół jest sosnowy”. Oba takie sądy mogą być mylne, jeżeli dany stół jest np. orzechowy.

Zdarzają się czasem pozory przeciwieństwa między sądami, podczas gdy naprawdę zachodzi tylko nieporozumienie między tymi, którzy się niepotrzebnie spierają. Tak np. pierwszy z tych dwóch nauczycieli, którzy się spierali przed chwilą o pilność uczniów pewnej klasy, mógł mieć na myśli ich pilność w zakresie swojego przedmiotu, np. w geografii, a drugi myślał o swoim przedmiocie i może też słusznie twierdził, że żaden z tych uczniów nie jest pilny, ale w rachunkach. Wtedy sądy ich obu mogły być prawdziwe, ale to nie były sądy przeciwne, tylko ich powiedzenia były przeciwne i stwarzały pozory przeciwieństwa między sądami. A gdy chodzi o stoły, to też ktoś jeden mógł myśleć o samej powierzchni blatu stołowego, kiedy mówił wyrazy „stół dębowy”, a drugi brał wtedy pod uwagę i blat, i nogi. Wtedy ich powiedzenia były przeciwne, ale między ich sądami nie było przeciwieństwa. Mogły być oba prawdziwe. Stół mógł mieć na powierzchni fornir dębowy, a całą konstrukcję sosnową. Wypadało się porozumieć co do znaczenia wyrazów albo od razu mówić wyraźniej.

Prawda, FałszMiędzy dwoma sądami może zachodzić jeszcze inny stosunek logiczny. A mianowicie wtedy, gdy prawdziwość pierwszego sądu pociąga za sobą prawdziwość drugiego, a fałszywość drugiego pociąga za sobą fałsz pierwszego, ale nie na odwrót. To jest stosunek wynikania. Pierwszy z takich dwóch sądów nazywa się racją, a drugi następstwem. Na przykład: 1) „ktoś kupił wczoraj i zapłacił cetnar[4] drzewa”, więc: 2) „miał przy sobie pieniądze”. Tu widać, że jeżeli ktoś naprawdę kupił ten cetnar i zapłacił, to musiał mieć pieniądze, i to, że jeżeli nieprawdą jest, jakoby miał pieniądze, to nieprawdą musi być, że coś kupił i zapłacił. Ale nie na odwrót. Bo jeżeli jest prawdą, że pieniądze miał, to jeszcze nie musi być prawdą, że coś kupował i płacił. I to też widać, że jeśli nie jest prawdą, iż kupił i zapłacił, to nie musi być zaraz fałszem to, jakoby miał pieniądze. Mógł je przecież mieć, a nic nie kupować i nic nie płacić.

Taki sam stosunek zachodzi pomiędzy jakimkolwiek sądem ogólnym i szczegółowym o tych samych rzeczach. Np.: 1) „wszystkie zwierzęta oddychają” i 2) „przynajmniej niektóre zwierzęta oddychają”. Tu widać, iż z prawdziwości pierwszego sądu wynika prawdziwość drugiego, a to też, że gdyby fałszywy był sąd drugi, to musiałby być fałszywy pierwszy. Ten pierwszy uważamy za prawdziwy, ale nie dlatego tylko, że jest prawdziwy ten drugi. I gdyby nieprawdą było, że wszystkie zwierzęta oddychają, mogłoby nie być fałszem to, że tak robią przynajmniej niektóre. Bo na przykład prawdą jest, że niektóre zwierzęta latają, a z tego wcale nie wynika, żeby latały wszystkie, i to ostatnie nie jest prawdą.

Podobnie ma się rzecz z sądami przeczącymi ogólnym i szczegółowym. Jeżeli żaden przedmiot pewnego rodzaju nie ma pewnej cechy, to oczywiście i niektóre przedmioty tego rodzaju nie mogą tej cechy posiadać. I z tego, że jakiejś cechy nie posiadają niektóre przedmioty pewnego rodzaju, nie wynika wcale, żeby jej nie posiadały wszystkie. Tak już jest. Sąd ogólny o jakimś rodzaju przedmiotów jest racją dla sądu szczegółowego o tym samym rodzaju rzeczy, a sąd szczegółowy o nich jest następstwem sądu ogólnego. Dlatego, kto dobrze uważa i pamięta, nie zaprzecza w szczególności temu, na co się zgodził w ogólności. Co innego, gdy stwierdzamy jakieś wyjątki od reguły lub zasady ogólnej. Wtedy mówimy np., że jutro oddajemy do prania wszystką bieliznę z wyjątkiem tych rzeczy, które leżą w szafie na półkach. Albo że w wojsku służyć muszą wszyscy z wyjątkiem tych, których władze wojskowe uznają za niezdolnych. W takich razach myślimy nie o wszystkich przedmiotach pewnego rodzaju, tylko o wszystkich z wyjątkami. A to jest coś innego niż „wszyscy bez wyjątku”. W mowie potocznej nie zawsze na to uważamy. Tak się może trafiło i temu, który mówił, że po widowisku wszyscy poszli do domu, a niektórzy zostali jeszcze. Być może, miał na myśli „wszystkich z wyjątkami”, a nie „wszystkich w znaczeniu ścisłym”. SłowoTrudno ręczyć za to, co ma na myśli ktoś, kto się wyraża nieściśle.

Rozumowanie

Wymieniliśmy kilka rodzajów sądów zostających w związku logicznym i wiemy, że prawdziwość jednego sądu zależy nieraz od prawdziwości lub fałszywości sądów innych, a tak samo fałszywość jednych sądów pociąga za sobą nieuchronnie fałszywość lub prawdziwość sądów innych. Jeden łatwiej potrafi dostrzec związek logiczny między dwoma rodzajami sądów, a drugi mniej łatwo, bo albo nie uważa, albo zapomina o sądzie pierwszym, kiedy wydaje sąd drugi. Ale kto uważa i pamięta, ten nie wydaje sądów sprzecznych ani przeciwnych sobie i jeżeli wydał jeden sąd z takich dwóch, to już dzięki temu wystrzega się drugiego z nich, bo go z góry uważa za fałszywy. I jeżeli uznał za prawdę jakąś rację, to uznaje za prawdę i jej następstwo, a jeżeli widzi, że z pewnego sądu wynika fałszywe następstwo, to jest pewny, że i ten sąd musiał być fałszywy. Nigdy nie mówi: „Pan ma słuszność, ale ja się z panem nie zgadzam”, bo to jedno zaprzecza drugiemu. Chyba żeby jeden sąd uważał za słuszny, a nie zgadzał się na jakiś inny.

Rozum, Sen, Choroba, AlkoholU każdego, kto uważa i dobrze pamięta, zjawia się przy wydawaniu jakiegokolwiek sądu na serio lub „na niby” gotowość do wydawania sądów będących następstwami sądu wydawanego i do odrzucania, do zaprzeczania sądom, które by były z sądem wydawanym sprzeczne. Możemy to wyrazić krótko, mówiąc, że sądy i supozycje człowieka przytomnego w całej pełni posiadają tendencję[5] logiczną. „Przytomnym być” to tyle, co „uważać i pamiętać”. Kiedy jesteśmy roztargnieni albo zasypiamy powoli, wtedy zanikają tendencje logiczne naszych sądów i znosimy spokojnie, gdy ktoś mówi lub czyta zdania sprzeczne, nie dostrzegamy związków logicznych, mylimy się i plączemy w rachunkach. Przytomność ma różne stopnie. Dlatego mówimy tu o człowieku przytomnym w całej pełni. Przytomność obniża się przy wielkim zmęczeniu, wyczerpaniu, wzburzeniu, w gorączce, w chorobach psychicznych, pod wpływem trucizn, jak np. alkoholu. Trudno samemu rozstrzygać o tym w danej chwili, czy jesteśmy przytomni w całej pełni, czy nie bardzo. Łatwiej ktoś drugi potrafi to zauważyć, kiedy się nam język zaczyna plątać, albo nas coś przebudzi i do przytomności doprowadzi, choćby na chwilę. Dopiero w przypomnieniu nieraz dostrzegamy, żeśmy nie chwytali związków w tekście czytanym wczoraj do poduszki albo w monotonnym opowiadaniu przydługim, w którym się opowiadający zacinał i plątał, i cedził.

Rozum, FilozofOtóż dostrzegać związek logiczny między dwoma sądami i dzięki temu uważać za prawdziwy lub za fałszywy sąd drugi, skoro się wydało lub zrozumiało sąd inny — to znaczy tyle, co rozumować. Rozumuje każdy, kto dostrzega, co z danego sądu wynika i na czym się dany sąd opiera. Dostrzegać następstwo danego sądu i wysnuwać je, to znaczy wnioskować. A dostrzegać rację pewnego sądu i na niej prawdziwość danego sądu opierać — znaczy dowodzić lub tłumaczyć. Kto wnioskuje, ten mówi: „a więc”. Kto dowodzi lub tłumaczy zjawiska, ten mówi: „ponieważ” lub: „dlatego że”. Czasem ktoś mówi: „znakiem tego, że”. Ale to zwrot niewłaściwy, bo nie wiadomo, o co w nim chodzi. Czy o to, że coś jest skutkiem czy objawem, czy znakiem, czy następstwem czegoś innego, czy też chodzi jeszcze o inne rzeczy. Rozum, FilozofWe wnioskowaniu sąd będący racją nazywa się przesłanką, a ten, który jest następstwem, nazywa się wnioskiem. Wzywamy kogoś do wnioskowania słowami: „I co z tego wynika?”. W dowodzeniu następstwo nazywa się tezą, a racja nazywa się argumentem. W tłumaczeniu zjawisk racja to hipoteza. Pytamy o argumenty, mówiąc: „Z czegóż to wynika?” lub: „Na czym się to twierdzenie opiera?”. O hipotezy pytamy: „Czemu tak jest?”, „Czym się to tłumaczy?”. Wiemy już, że człowiek uważny zgadza się na wniosek, jeżeli się zgodził na przesłanki i jeżeli sądy, które rozpatruje, zostają naprawdę w stosunku wynikania. I to wiemy, że gdy ktoś stawia pewną tezę i próbuje jej dowodzić, to każdy uważny człowiek o dobrej pamięci będzie musiał uznać słuszność jego tezy, jeśli podane argumenty będą prawdziwe i jeśli teza z nich naprawdę wynika. Jeżeli by teza była prawdziwa, nie świadczy to jeszcze o prawdziwości argumentów, na których ją ktoś opiera. Choćby nawet zachodził związek wynikania między nią a argumentem. Niejeden opiera prawdziwą tezę na fałszywym argumencie. Błądzenie, FilozofZauważył np. w pociągu kilku Duńczyków brunetów i potem próbuje dowodzić, że dlatego 2) niektórzy Duńczycy są brunetami, ponieważ 1) wszyscy Duńczycy mają czarne włosy. A to jest jaskrawa nieprawda. Tutaj sąd ogólny był racją dla sądu szczegółowego, ale był fałszywy. Nasz podróżny popełnił w swym dowodzeniu błąd rzeczowy. Nie popełnił błędu formalnego. Byłby popełnił błąd formalny, gdyby był dowodził, na przykład, w ten sposób: „Ci tutaj są brunetami, ponieważ tamci, spotkani przed chwilą, byli blondynami”. Tu brakłoby związku logicznego między jego dwoma sądami i on nie umiałby rozumnie odpowiedzieć na pytanie: „Co ma jedno do drugiego?”.

Ktokolwiek podaje jako argument twierdzenie, które nie może być racją dla danego sądu, ten popełnia błąd formalny. Tak samo kto jako wniosek wysnuwa sąd, który nie może wynikać z jego przesłanki. Zawsze błąd formalny polega na mylnym dostrzeżeniu związku logicznego tam, gdzie go wcale nie ma, albo na przeoczeniu związku logicznego tam, gdzie on naprawdę zachodzi. Błąd rzeczowy to po prostu sąd mylny o przedmiocie, o którym się mówi. Rozumowanie może być błędne rzeczowo, a poprawne formalnie i może być wolne od błędu rzeczowego, a zawierać błąd formalny. Może być w końcu błędne i rzeczowo, i formalnie. Wszystkie trzy rodzaje błędów zdarzają się tym, którzy nie potrafią dobrze uważać i nie pamiętają swoich i cudzych myśli poprzednich.

Rozumowanie pośrednie

PrawdaNie każdy nasz sąd wymaga racji, jeżeli mamy go uznać za prawdziwy. Są takie sądy, których prawdziwość narzuca się nieodparcie każdemu, kto tylko dany sąd zrozumie. Takie sądy nazywają się bezpośrednio oczywiste. Na przykład: „Dwie ilości, z których każda jest równa tej samej ilości trzeciej, są między sobą równe”. Albo: „Żaden przedmiot nie posiada cech, które się wykluczają”. Albo: „Co się stało, to się nie odstanie”. Albo: „Co dotyczy każdego z osobna, to dotyczy i niektórych”. Tego rodzaju sądy wydajemy bez obawy pomyłki i to słuszne, bo to już tak jest naprawdę. Takich sądów bezpośrednio oczywistych nie ma dużo, ale nie podobna ich wszystkich wyliczyć i porachować. Tym bardziej, jeżeli do sądów bezpośrednio oczywistych zaliczymy sądy dotyczące treści wrażeń doznawanych w danej chwili, jak np.: „czuję teraz zimno, widzę kolor czerwony, słyszę głos jakiś” itp. Ale ten rodzaj sądów bywa też i mylny; wiemy o złudzeniach zmysłowych i to wiemy, że nieraz trudno jest ująć i nazwać to, czego doznajemy. Wiedza, FilozofKtóre sądy i jakiego rodzaju są oczywiste i pewne, a które nie są pewne, a więc którym przeczyć nie można i nie należy, a o których wątpić można, tym zajmuje się teoria poznania[6]. My tutaj stwierdzamy tylko, że oprócz sądów oczywistych są liczne sądy nieoczywiste, czyli takie, które się nam nie narzucają same przez się, a uważamy je za prawdziwe dlatego, że są następstwami logicznymi, czyli wynikają z innych sądów, które już uważamy za niewątpliwie prawdziwe. Wykazywać, że jakiś sąd jest logicznym następstwem innego sądu prawdziwego, znaczy: uzasadniać dany sąd. Inaczej to samo: podawać dla niego niewątpliwą rację.

Rozum, Wiedza, FilozofJeżeli rację jakiegoś sądu stanowi jeden tylko sąd inny, wtedy mówimy, że dany sąd wynika bezpośrednio z tego innego, i takie rozumowanie nazywamy bezpośrednim. Jeżeli zaś dany sąd nieoczywisty wymaga do swego uzasadnienia dwóch sądów albo więcej, mówimy o rozumowaniu pośrednim. Nauka logiki podaje liczne wzory rozumowania pośredniego. My się tym nie będziemy zajmowali, poprzestaniemy na przykładzie najprostszym.

Wiemy, że: 1) wszystkie zwierzęta żyjące stale pod wodą oddychają skrzelami. I wiemy, że: 2) raki żyją stale pod wodą. Pytamy się, co z tych dwóch przesłanek wynika? Wynika z koniecznością wniosek, że raki oddychają skrzelami. Było to rozumowanie pośrednie, bo wniosek opierał się na dwóch przesłankach. Było to też rozumowanie dedukcyjne[7], bośmy w nim pewną znaną ogólną regułę stosowali do pewnej grupy przedmiotów.

A bywa i na odwrót. Naprzód czynimy szereg spostrzeżeń jednostkowych na jakimś rodzaju przedmiotów, a potem pytamy się, czym się te spostrzeżenia tłumaczą, to znaczy: jaki sąd ogólny mógłby być wspólną racją dla sądów zawartych w naszych licznych spostrzeżeniach. Szukamy takiego sądu i jeżeli się nam jakiś sąd wydaje dobry do tego celu, przyjmujemy go na razie jako hipotezę, mającą poczynione spostrzeżenia tłumaczyć. Nie możemy jej być pewni, bo świata nie znamy dostatecznie, więc musimy czynić spostrzeżenia dalej i czekać, czy się nie zdarzy jakieś spostrzeżenie, które będzie z daną hipotezą sprzeczne. Gdyby się takie spostrzeżenie trafiło, odrzucamy dotychczasową hipotezę, a oglądamy się za inną, lepszą, bo zgodną z nowym i starymi spostrzeżeniami. Tak np. w dawnych wiekach ludzie spostrzegali, że jakkolwiekby ktoś daleko pojechał, zawsze, stojąc pod gołym niebem, widzi najbliższą sobie okolicę jako okrągłą tarczę pod kopułą nieba, a na tej tarczy góry, doliny, rzeki i jeziora. I nigdy nie można dojechać do obwodu tej tarczy. Więc pytali się, czemu to tak wygląda wszędzie i czym się to tłumaczy. Odpowiadali sobie na to pytanie, mówiąc, że chyba cała ziemia jest wielką tarczą płaską i okrągłą, z górami, dolinami i rzekami, a że jest bardzo rozległa, dlatego nie można dojechać do granicy kopuły niebieskiej i ziemi lub nieba i morza. Długi czas zadowalali się tą hipotezą. Tymczasem inni spostrzegali dalej i zauważyli, że gdy statek odpływa daleko, wtedy naprzód się chowa pod horyzontem jego kadłub, a maszty jeszcze widać. Maszty chowają się później. Skądże to zjawisko? Jeżeliby powierzchnia morza była wielką płaszczyzną naprawdę, nie mogłyby się okręty odjeżdżające chować powoli, jakby zachodziły za pagórek. Wobec tego porzucili hipotezę o płaskości ziemi, a przyjęli inną, lepszą. Pomyśleli sobie, że ziemia musi być bardzo wielką kulą i jej powierzchnia — zarówno lądów, jak i mórz — nie jest płaska, tylko jest okrągła, kulista. To przypuszczenie, czyli hipoteza, lepiej tłumaczyło poczynione spostrzeżenia niż hipoteza poprzednia. Oprócz tego tłumaczyło i to, że cień ziemi, rzucony na księżyc, jest okrągły, jak zwykle cień kuli. Z hipotezy, iż ziemia jest wielką kulą, wynikało i to, że płynąc wciąż przed siebie na zachód, można by ziemię opłynąć naokoło i wrócić do domu z przeciwnej strony. To się naprawdę udało, chociaż dopiero po wielu wiekach. Dziś nie znamy żadnego zjawiska, które by się nie dało pogodzić z hipotezą kulistości ziemi, a wszystkie dotychczas poznane zjawiska godzą się z nią doskonałe i jasno z niej wynikają. Znaczy to, że przemawiają za nią. Dlatego i dziś uważamy tę hipotezę za niezmiernie prawdopodobną[8].

W nauce o życiu na ziemi przyjęto hipotezę ewolucyjną, to znaczy twierdzenie, że dzisiejsze istoty żywe są potomkami istot żywych z dawnych okresów. Przy pomocy tej hipotezy tłumaczy się niezliczoną ilość spostrzeżeń dotyczących szkieletów zwierzęcych odkopywanych z ziemi i mnóstwo spostrzeżeń dotyczących budowy ciała dzisiejszych zwierząt i roślin. W fizyce zjawiska świetlne nie są do dziś dostatecznie wytłumaczone, bo jedne z nich tak wyglądają, jakby światło było pewnym ruchem falowym, a inne tak, jak gdyby ciała świecące wyrzucały z siebie bardzo małe bryłki. Te dwie hipotezy nie są ze sobą zgodne, tylko sobie przeciwne, więc obie nie mogą być zarazem prawdziwe, a nie udało się dotąd wymyślić żadnej, która by mogła wytłumaczyć wszystkie zjawiska świetlne. Ale miejmy nadzieję, że kiedyś się taka znajdzie.

Rozum, Wiedza, FilozofDoszukiwanie się wspólnej racji dla wielu spostrzeżeń nazywa się rozumowaniem indukcyjnym. Jest to droga od następstw do racji — prawdopodobnej. W nauce logiki można znaleźć opis sposobów tworzenia hipotez naukowych i sprawdzania ich również.

Inteligencja

Tak się nazywa zdolność do trafnego rozumowania. Rozum, Filozof, WiedzaInteligentny nazywa się człowiek nie ten, który wciąż rozumuje, bo takiego nie ma. Każdy czasem śpi twardo, a czasem bawi się i odpoczywa. Wtedy nie musi rozumować. Inteligentny jest ten, kto w razie potrzeby i mając niezbędne wiadomości, potrafi z danych mu przesłanek wysnuć wnioski, które z nich naprawdę wynikają i do danych mu następstw znaleźć prawdziwą rację, czyli wytłumaczyć sobie czynione spostrzeżenia przy pomocy prawdopodobnej hipotezy.

Nie każdy robi to z jednakową łatwością, co widać raz po tym, co ktoś mówi, a kiedy indziej poznać po tym, co i jak kto robi. Inteligentne i nieinteligentne mogą być albo czyjeś słowa, albo czyjeś zachowanie się.

Rozum, PamięćWidać już z określenia inteligencji, że człowiek, który się nią ma odznaczać, musi być zdolny do skupiania uwagi i mieć dobrą pamięć; jego sądy muszą mieć żywą tendencję logiczną i ten człowiek musi łatwo dostrzegać związki logiczne między sądami, stosunki między pojęciami, podobieństwa i różnice między przedmiotami i zdarzeniami. Wtedy łatwiej mu rozumieć to, z czym ma do czynienia. Po łacinie wyraz „intelligo” znaczy właśnie „rozumiem”.

Rozum, Siła, Dobro, ZłoInteligencja jest znakomitym narzędziem, które pozwala człowiekowi utrzymać się i zwyciężać w walce o życie z przyrodą i ze złymi ludźmi. Dobremu człowiekowi pozwala czynić dobrze, nie przynosząc przy tym szkody, bo mu pozwala często dostrzegać pośrednio następstwa swoich i cudzych czynów. Nikogo sama inteligencja nie zrobi człowiekiem lepszym pod każdym względem. Wiemy, że i zbrodniarze bywają bardzo inteligentni i przez to są tym bardziej niebezpieczni.

Rozum, PamięćInteligencja nie obejdzie się bez pamięci, ale sama pamięć nie stanowi inteligencji. Wiemy, że pamięć może być i mechaniczna. Dlatego chcąc się przekonać, czy jeden człowiek jest bardziej inteligentny niż drugi, nie patrz na to, czy jeden z nich więcej potrafi zapamiętać i więcej posiada wiadomości niż drugi, bo to ci nic nie powie o jego inteligencji. I o tym pamiętaj, że stopnia inteligencji nie można oznaczać w żadnych jednostkach i nie można z sensem powiedzieć, że ktoś jest dwa razy lub trzy razy tak inteligentny jak drugi, ani też tego, że inteligencja jednej osoby przerasta inteligencję drugiej o jakiś ułamek. W życiu rozróżniamy ludzi bardziej bystrych i raczej tępych, znamy ludzi upośledzonych i wyjątkowo sprawnych umysłowo, ale te oceny muszą zostać ogólnikowe, bo miarki dla inteligencji nie posiadamy.

Próby pomiarów inteligencji

Mimo to stosują od kilkudziesięciu lat w Europie i w Ameryce szeregi zadań służących do porównywania inteligencji młodzieży i ludzi chorych psychicznie, ujmują wyniki tych badań w liczby. Krótkie egzaminy, służące do stwierdzania, czy ktoś posiada pewną dyspozycję[9] psychiczną, nazywają się z angielska testami. Najbardziej rozpowszechniony zbiór testów do badania inteligencji pochodzi od Bineta i Simona, psychologów francuskich, którzy go ogłosili w roku 1905. Psycholog amerykański Terman przerobił ten zbiór w roku 1914; jego pracę przełożyła w roku 1926 na język polski Janina Bużycka, później ją poprawił prof. Baley i dziś ją stosują w szkołach i w poradniach młodzieżowych.

Nie można tu szczegółowo omawiać testów zawartych w tej skali, bo każdy test powinien być niespodzianką dla osoby badanej, aby nie podawała bezmyślnie odpowiedzi wyuczonej na pamięć i dobrze znanej. Oprócz tego osoba badana nie powinna się niechętnie odnosić do sposobu badania. W końcu trzeba krytykę obecnie stosowanych testów zostawić specjalistom, którzy się zajmują psychologią dziecka.

W każdym razie obliczenia i cyfry[10] stosowane w tych badaniach nie mają znaczenia ścisłego, nie można ich brać dosłownie, tylko mniej więcej, w przybliżeniu jakimś, jako wskazówkę ogólnikową. Rozum, NaukaTak np. tak zwany iloraz inteligencji uzyskują, dzieląc tak zwany wiek inteligencji przez wiek życia, obliczony w miesiącach. Do tego celu wiek inteligencji też wypada obliczać w miesiącach. Robią to na podstawie umowy i dostateczną odpowiedź osoby badanej na każde z osobna pytanie, zawarte w zbiorze Termana, liczą jako trzy miesiące wieku inteligencji albo jako dwa, jeżeli chodzi o dzieci do lat dziesięciu, a dla starszych po siedem i pół miesiąca, albo i po dziewięć miesięcy wieku umysłowego. U normalnych dzieci wiek inteligencji, obliczony w ten sposób, ma się zgadzać z wiekiem życia i iloraz inteligencji wynosi u nich 1. Tę jedynkę mnożą przez sto, aby nie pisać ułamków. U niedorozwiniętych wypada ten iloraz niższy od stu, bo dają mniej dobrych odpowiedzi, niż im zadano pytań; u rozwiniętych nad wiek — wyższy od stu, bo oprócz zadań przeznaczonych dla ich wieku rozwiązują niektóre zadania dla starszych. Łatwo zgadnąć, że u milczących, przestraszonych, roztargnionych, niechętnych, nieznających dobrze języka muszą wypadać ilorazy niskie, które nie będą obrazem ich inteligencji. W każdym razie bardzo niski i bardzo wysoki iloraz inteligencji powinien zwrócić uwagę na rozwój umysłowy osoby badanej wtedy, gdy osoba badająca budzi zaufanie. A gdy go nie budzi — również.

Sugestia

Skąd się biorą nasze przekonania i na czym się opierają? Mówiliśmy już, że w każdym spostrzeżeniu są zawarte sądy. Uważamy je za prawdziwe w chwili spostrzegania i uważamy je za prawdziwe później, pokąd nie zauważymy między nimi jakiejś sprzeczności. Wtedy poprawiamy sobie nieraz w myśli dawne spostrzeżenia i jeden z dwóch sądów sprzecznych uważamy za fałszywy, a przy drugim zostajemy. To wtedy, gdy uważamy, pamiętamy i myślimy przytomnie, co się nie zawsze zdarza i udaje. Tylko człowiek bardzo przytomny unika sądów sprzecznych i czuje, że któryś z nich musi być mylny, a drugi prawdziwy. To zdanie nazywa się psychologiczną zasadą sprzeczności. Ono tłumaczy to, że nie zawsze zostajemy przy jakimś spostrzeżeniu, które się nam kiedyś trafiło, tylko je kontrolujemy i nieraz poprawiamy przy pomocy spostrzeżeń dalszych. Spostrzeżenia własne kontrolujemy przy pomocy spostrzeżeń cudzych i na tych już zwykliśmy polegać, choć wiemy, że zdarzają się złudzenia, a nawet halucynacje[11] zbiorowe. Sądy zawarte w spostrzeżeniach narzucają się nam jako prawdziwe i jeżeli są dostatecznie skontrolowane, nie budzą wątpliwości.

Narzucają się nam też jako niewątpliwe sądy bezpośrednio oczywiste, o których była już mowa niedawno. Inne sądy uważamy za prawdziwe dlatego, że wynikają jako następstwa logiczne z sądów, którym nie potrafimy zaprzeczać. Takie sądy nazywają się uzasadnione. Są oparte na swoich racjach. Inne dobieramy sobie jako prawdopodobne racje do spostrzeżeń.

Prawda, Fałsz, Rozum, WiaraAle są jeszcze inne w naszym życiu intelektualnym, które nie są ani bezpośrednio oczywiste, ani uzasadnione, ani prawdopodobne, a jednak je niejeden uważa za prawdziwe i trzyma się ich tak, jakby były oczywiste. To są sądy oparte na pobudkach uczuciowych i na czyimś wpływie osobistym. Tak np. ktoś uważa pewnego człowieka za zdolnego do niegodziwości ostatniej, a nie potrafi tego poważnie uzasadnić i w rozmowie pokazuje się, że ten ujemny sąd nie opiera się u niego na przesłankach, tylko na nienawiści i pogardzie osobistej lub grupowej. Gdyby ten ktoś umiał siebie obserwować i chciał być szczery, powiedziałby: „Źle myślę o tym człowieku, bo go nie znoszę i gardzę nim. On jest zły, bo jest wstrętny”. To, oczywiście, nie jest racja wystarczająca do ujemnej oceny etycznej człowieka i ta ocena jest nierzeczowa, bo jest oparta na pobudkach, a nie na wystarczających argumentach. Podobnie bywa pod wpływem uczuć miłości i czci. „On jest znakomity i szlachetny, bo jest mój i najdroższy”, to by był szczery wyraz niejednej oceny dodatniej opartej na uczuciu, a nie uzasadnionej logicznie. Przez długie wieki beznożna i nieszkodliwa jaszczurka, zwana padalcem, uchodziła za niecierpliwe i groźne stworzenie dlatego tylko, że jest podobna do węża, więc się jej ludzie bali — niepotrzebnie. Przesąd o szkodliwości padalców był nieuzasadniony, a był oparty na uczuciu obawy.

Rozum, Wiara, Prawda, Fałsz, Filozof, NienawiśćProstowanie ludzkich sądów opartych na uczuciach to sprawa trudna i delikatna. Ludzie łatwo zaczynają nienawidzić tego, który im próbuje wykazywać mylność lub bezpodstawność sądów opartych na uczuciach. Łatwiej ich sobie zrazić niż przekonać, jeżeli ich tendencje logiczne nie są dość żywe, a uczucia są gorące.

ModaW końcu jeszcze jedno źródło ludzkich sądów nieoczywistych trzeba wymienić, a jest nim wpływ osobisty osób drugich, zwany sugestią albo wpływem sugestywnym. Najłatwiej go zauważyć u osób, które innym imponują, wydają się potężne, wpływowe, bogate, niezależne, piękne, cieszą się czcią i życzliwością ludzką. Wielu ludzi objawia gotowość do tego, żeby takich ludzi naśladować, spełniać ich życzenia i uznawać za prawdziwe te sądy, które tamci objawiają słowami lub zachowaniem się. Taki wpływ ma nieraz w szkole chłopak odznaczający się siłą fizyczną i odwagą, czasem nauczyciel, którego dzieci lubią, a boją się go równocześnie; taki wpływ na dorosłych mają popularni wodzowie, gazety, druki, afisze, sławni ludzie, piękne kobiety. Dlatego na afiszach i drukach reklamowych tak często piękna kobieta zachwala towar jakiś i własnym podpisem stwierdza, że go używa stale. Na flaszkach atramentu widnieje fotografia i podpis wielkiego poety, aby pobudzać do naśladowania go przez pisanie tym samym atramentem, co i on. Za czasów Franciszka Józefa i Wilhelma I woźni w urzędach nosili bokobrody po cesarsku, a eleganci całej Europy ubierali się tak jak książę Walii, późniejszy Edward VII. Nie dopinali nawet ostatniego guzika u kamizelki, ponieważ go raz odpiął książę Walii po jakimś obfitym obiedzie.

Prawda, Uroda, Słowo, ObyczajePo sklepach kazano podczas okupacji niemieckiej wywieszać hasła agitacyjne w pięknych ramkach, aby się wydawały prawdami i pobudzały do działania, chociaż żadne zdanie nie staje się prawdziwe ani uzasadnione przez to, że się je wydrukuje ozdobnie i wywiesi na ulicy lub w sklepie. A jednak może przez to działać sugestywnie i udzielać się tym, którzy je czytają. Taki wpływ wywiera często każde słowo drukowane. Stąd doniosłość gazet. Niebywałe niedorzeczności ludzie powtarzali i przed wojną, i podczas wojny, nie uzasadniając ich niczym więcej nad to, że tak mówią na mieście albo piszą w gazecie. Łatwo zauważyć osoby zakochane, które są żywym echem przedmiotów swojej miłości, i zagorzałych czcicieli, którzy powtarzają za przedmiotami swojej czci jak „za panią matką”. A na pytanie o argumenty odpowiadają: „On sam tak powiedział — więc już tak jest”. Na poparcie swego zdania przytacza niejeden liczne nazwiska autorów, których może i sam nie czytał, a na pewno nie czytali ich jego słuchacze i samo przytoczenie sławnych nazwisk zastępuje niejednemu argumenty rzeczowe.

Wiedza, Rozum, Siła, Niewola, Pozory, ZwycięstwoCzemu tak jest? Czemu ludzie niektórzy tak łatwo ulegają sugestii i żywią przekonania, których nie umieją uzasadniać rzeczowo? Często pochodzi to stąd, że nie ufają własnemu zdaniu i czują, że nie stać ich na własny sąd, a wstydzą się do tego przyznać, więc przejmują się sądami drugich, które spotykają. Mówią wtedy: „Ja tam nie wiem, ale tak słyszałem”. Czasem chcą pokazać, że się znają na jakiejś dziedzinie, np. na obrazach, na literaturze, na medycynie, na prawie, na fizyce, na zwyczajach towarzyskich, więc naśladują zdania zasłyszane i wprawiają się w stan przekonania nieszczerego, bo to ich podnosi we własnych oczach albo w cudzych. Chwalą i ganią nieszczerze to, co chwali i gani ktoś, kto im imponuje. Takich nazywają ludzie snobami. Czasem pragną sobie pozyskać względy i zbliżyć się do kogoś przez upodobnienie się do niego, czasem nie chcą odbijać od otoczenia, czasem dla świętego spokoju żywią zrazu pewne supozycje, a później i przekonania przejęte od innych ludzi, bez dowodu. Byłyby to więc również sądy oparte na uczuciach, a nie na racjach.

Moda, PlotkaSugestia ma nad wyraz doniosłe znaczenie, gdy chodzi o powstawanie i szerzenie się mód, prądów i szkół artystycznych, literackich i politycznych. Sugestią posługują się często lekarze, kiedy z powodzeniem wmawiają w pacjenta poprawę stanu zdrowia, i wychowawcy, kiedy wpływem osobistym skłaniają dzieci do wierzenia im, do posłuszeństwa i naśladowania ich w postępowaniu.

Rozum, FilozofOporność przeciw sugestii, a więc gotowość do uznawania tylko sądów uzasadnionych oraz oczywistych bezpośrednio, nazywa się krytycyzmem.

Wiara, Rozum, Strach, Choroba, Szaleniec, Nienawiść, Polityka, Przyjaźń, WrógPrzeciwstawieniem sugestywności jest tzw. negatywizm. Ten występuje najwyraźniej u pewnych chorych psychicznie. Taki pacjent nie wierzy w nic, co mu lekarz powie, i co tylko z jego ust usłyszy, to uważa za fałsz. Dlatego tylko, że to powiedział lekarz. Gdy go lekarz prosi, żeby przyszedł bliżej, on się oddala, gdy ma drzwi zamknąć, on je otwiera szeroko, gdy ma stać, siada i siedzi uparcie, gdy go zapytują, milczy, a gdy mu każą milczeć, mówi. Zachowuje się „jak na złość”. Widocznie broni się w ten sposób od wpływu lekarza albo go chce rozgniewać, zaatakować, poniżyć. Coś podobnego zauważyć można u osób obrażonych, złych, mściwych, gdy stosunki osobiste są popsute albo podminowane. Tak się niektórzy ludzie odnoszą do gazet przeciwnego obozu i do grup ludzkich, których nienawidzą. Krytycyzm chroni od sugestywności i od negatywizmu.

O autosugestii mówimy, gdy ktoś sam w siebie wmawia i podtrzymuje w sobie jakieś przekonanie nieoczywiste. Ono może dotyczyć czegoś poza człowiekiem, albo, co się najczęściej zdarza, dotyczy stanu własnego ciała. Tak np. bywa, że ktoś wmawia w siebie osłabienie ogólne, bezwład rąk, niemożność mówienia, brak apetytu, kiedy lekarze nie mogą stwierdzić żadnego powodu do tych objawów.

Słowo, LekarzZ drugiej strony niektórzy zalecają skarżącym się na cierpienia pozbawione widocznego powodu leczenie się przy pomocy autosugestii. Tak np. znany aptekarz francuski, Coué, doradzał takim cierpiącym i ludziom przygnębionym powtarzać kilkadziesiąt razy z rzędu co dzień: „To mija, to przejdzie”. I to pomagało.

SenSen hipnotyczny albo hipnoza jest też wytworem sugestii. Usypiacz wmawia w człowieka, który się chce temu poddać, a leży lub siedzi w wygodnym fotelu, że za chwilę uśnie. Każe mu tymczasem patrzeć w jakiś punkt świecący albo usypiaczowi między oczy i mówi mu z cicha a tonem przekonującym, że już mu się powieki zamykają, zaciskają, że mu głowa cięży, a senność rozchodzi się po ciele. Następnie, że oczu otworzyć nie potrafi, że mu ręce bezwładnie opadają i zwisają, a potem że się roztworzyć nie dają, tak się zacisnęły mocno. Wielu ludzi wtedy zapada istotnie w osobliwy sen, nie tracąc porozumienia z hipnotyzerem. Słuchają go wtedy ślepo i wierzą mu. Pozwalają w siebie wmówić, że kartofel to jabłko, że dotykający ich ołówek to zapalony papieros, że jadą pociągiem lub samolotem, że są małymi dziećmi, że ktoś obecny wyszedł z pokoju i wiele innych rzeczy. Jeszcze po zbudzeniu się wykonują rozkazy dane im podczas hipnozy, choćby były dziwaczne. Nie można jednak nikogo przez hipnozę zmusić do zbrodni, której by i sam, bez hipnozy, nie był wykonał. Dawniej stosowali hipnozę lekarze dla odzwyczajenia ludzi od nałogów, dla poprawy w cierpieniach psychicznych, ale dziś to wyszło z mody, bo więcej przynosiło szkody niż pożytku. Hipnoza łatwo wchodziła w nałóg, poddawała usypianego w niewolę usypiacza i osłabiała wolę nawykłych do hipnozy. Nie powinni się nią bawić ludzie, którzy nie są lekarzami. Łatwo przy niej o oszukiwanie drugich i siebie samego, a także o wybuchy płaczów i krzyków, przerywane śmiechem, z którymi nie wiadomo co począć, i łatwo o szantaże[12] potem. Więc nigdy bez świadków i nigdy bez lekarza.

I. Pytania

1. Jakie sądy nazywają się prawdziwe, a jakie fałszywe?

2. Powiedz kilka zdań ogólnych twierdzących i kilka zdań szczegółowych przeczących i zastanów się, czy te zdania wyrażają twoje przekonania czy też supozycje.

3. W jakim stosunku zostają dwa pojęcia: „człowiek znajomy ci” i „człowiek uczciwy”? A te dwa: „człowiek” i „zwierzę”? A te: „koń” i „ptak”? A te: „kwadrat” i „czworobok”? A te dwa: „liść bobkowy” i „liść laurowy”?

4. Jaki sąd byłby sprzeczny z sądem: „jest już ciemno”?

5. Jaki stosunek zachodzi między sądem: „żadna żaba nie kąsa”, a drugim: „żaby zielone nie kąsają”?

6. Czy możesz z sensem połączyć dwa wymienione pod 5 zdania spójnikami takimi, jak „bo”, „ponieważ”, „dlatego że”, „a więc”?

7. Czy sąd, że ziemia obraca się naokoło słońca, jest zawarty w naszych spostrzeżeniach?

8. Kogo nazywają ludzie snobem?

9. Czy sugestywność u dzieci ułatwia ich wychowywanie czy utrudnia?

10. Czy kupiec traci czy zyskuje na tym, jeżeli ma wpływ sugestywny na klientów? Przez co go zyskuje, a przez co go traci?

II. Literatura

Kto by pragnął rozszerzyć sobie i pogłębić wiadomości zawarte w tym zeszycie, może zajrzeć między innymi do wymienionych tu książek:

Höfler Zawirski, Logika propedeutyczna, Lwów 1927.

Ajdukiewicz, Logiczne podstawy nauczania, Warszawa 1934.

Czeżowski, Główne zasady nauk filozoficznych, Toruń 1946.

Łukasiewicz, O nauce, Lwów.

Witwicki, Tadeusz, O potrzebie krytycyzmu, Lwów 1938.